Many hyperlinks are disabled.
Use anonymous login to enable hyperlinks.

Overview

Artifact ID:	22f4f550841c61347fc9eddb86d9cdbc1fe4201c
Page Name:	About ST_Subdivide()
Date:	2019-02-16 10:48:06
Original User:	sandro
Parent:	fc842978ba0d7b9506859f68d4e4e2db8628dc3a (diff)
Next	a027126d7e8b7b78fa1b0d9dd1e7071278910314

Content

ST_Subdivide(): a quick intro

back to index

About ST_Subdivide()

Since version 5.0.0 SpatiaLite supports ST_Subdivide(), an advanced SQL function already available on PostGIS.
The implementation is strictly similar in both Spatial DBMSes because on PostGIS the function is built on the top of the internal lwgeom library, and on SpatiaLite is built on the top of librttopo that simply is a more universal porting of lwgeom outside PostGIS.

A short rationale: processing huge geometries having an impressive number of Vertices (many thousands or even more) is an intrinsically slow process.
Subdividing them into many smaller parts (still preserving full topological consistency) usually helps to restore a satisfying processing speed. This is exactly the intended scope of ST_Subdivide():

this function will receive an input geometry (may well be a very huge one).
each Linestring or Polygon found within the input geometry will be then processed:
- all Linestrings or Polygons using a number of Vertices lesser or equal than the given threshold will be returned as they are.
- but all Linestrings or Polygons using an exceeding number of Vertices will be recursively split, until they'll be represented by a collection of elementary parts using no more than the required number of vertices.
at the end of the process the function will return a collection containing all elementary parts (a MultiLinestring or a MultiPolygon depending on the nature of the input geometry).

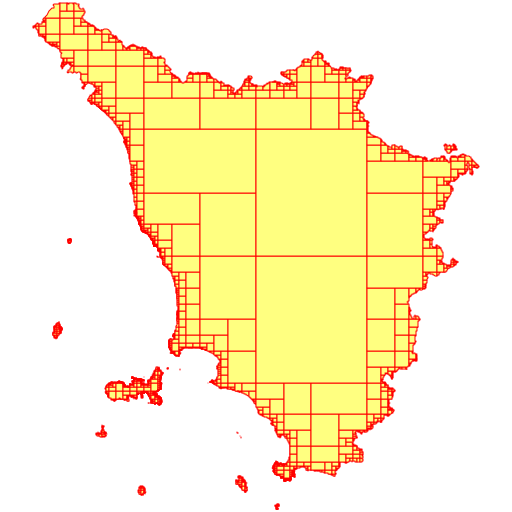
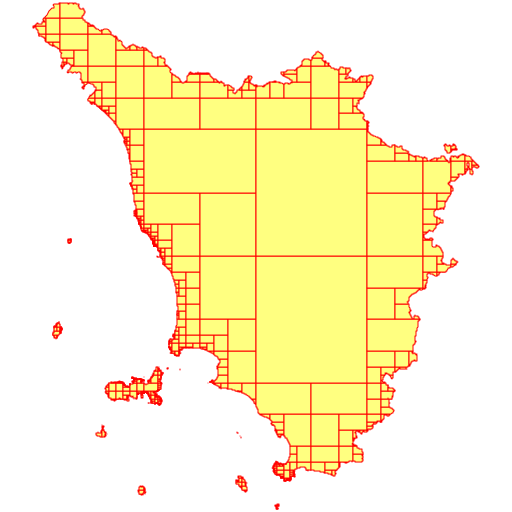
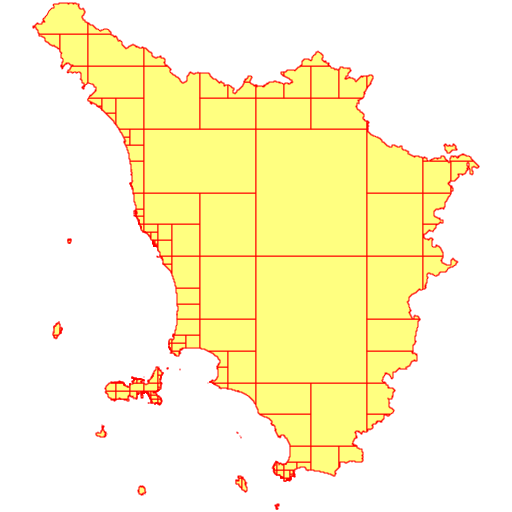
Basic Examples

The following examples are based on the am_reg_multipart Shapefile freely available for download from here (search for Ambiti Amministrativi - Administrative Boundaries).

This one supports a very accurate and precise map representation, and the main exterior ring has more than 100,000+ Vertices.
It's a very good example of a Geometry so huge to make extremely slow computing any Spatial operator (as e.g. ST_Intersects, ST_Touches, ST_Covers and so on).

SQL query

Visual Sample

SELECT ST_Subdivide(geometry) FROM tuscany;

in this first call no optional argument is specified, and thus ST_Subdivide() will implicitly assume the standard threshold of max 128 Vertices.

As the side figure shows, the returned result is a collection of about 4,300+ elementary parts.

SELECT ST_Subdivide(geometry, 512) FROM tuscany;

in this second call the optional argument is explicitly set, and ST_Subdivide() is now assuming a threshold of max 512 Vertices.

As the side figure shows, the returned result is a collection of about 1,800+ elementary parts.

SELECT ST_Subdivide(geometry, 2048) FROM tuscany;

in this third and final call the threshold is set to max 2,048 Vertices.

As shown by the figure, the returned result is now a collection containing just 1,200+ elementary parts.

Short conclusion

ST_Subdivide() is effectively capable to subdivide some nasty huge Geometry into a collection of many smaller parts much more reasonable to be handled.
And it's reasonably flexible and easy to be customized as required; you just have to set the most appropriate max. Vertices threshold.

However, a big caveat should be always considered about the multi-part collections returned by ST_Subdivide().
At least in the case of MultiPolygons any collection returned by ST_Subdivide() is inherently invalid, as the following SQL query demonstrates:

SELECT ST_IsValid(ST_Subdivide(geometry)) FROM tuscany;
---------
0

It's not at all difficult understanding why this happens.
Accordingly to standard OGC/SFS rules two single-part Polygons belonging to the same MultiPolygon are always forbidden to reciprocally touch.
More precisely: they can only touch on specific point(s), but they can never share a common boundary.

Caveat !!!

Never ever directly pass a Geometry of this kind to any Spatial operator such as ST_Intersects, ST_Touches, ST_Covers and alike.

This will certainly make crazy the GEOS library.
Incorrect results may easily follow.
And in the worst case some unexpected crash could eventually occur.

You have been warned !!!

Advanced Examples

Now we'll go to explore the real effectiveness of ST_Subdivide() in one of the most common Spatial Problems: identifying all intersections between a dataset of the POINT type and a huge Polygon/MultiPolygon.

During this second test we'll use the following datasets:

once again, the same administrative boundary of Tuscany we've already used before.
in the role of the POINT dataset we'll use the civici Shapefile (House Numbers) freely available for download from here (search for Grafo Stradale - Road Network).
This too is a huge dataset containing about 1.5 million points.

A first naive attempt

SELECT Count(*)
FROM civici AS c
LEFT JOIN tuscany AS t ON (ST_Intersects(c.geometry, t.geometry) = 1);


SELECT Count(*)
FROM civici AS c
LEFT JOIN tuscany AS t ON (ST_Intersects(c.geometry, t.geometry) = 1 
     AND c.rowid IN (
         SELECT rowid FROM SpatialIndex
         WHERE f_table_name = 'civici' AND search_frame = t.geometry));

The only difference between the above two SQL queries is in that the second one explicitly calls the Spatial Index.

Actual findings:

I was forced to prematurely abort the first test when I discovered that during the first half an hour it had made only a very little progress.
Accordingly to my estimated extrapolation, waiting for completion will had presumably required between 4 and 6 hours.
Definitely this isn't a practical solution for our problem.
the second test was, if possible, even slower than the first one.
And there is very good reason explaining for this; all Points to be checked fall inside the BBOX of Tuscany.
So the Spatial Index isn't of any possible help.
And even worst, querying the Spatial Index imposes a further overhead, thus requiring a longer time for absolutely nothing.
Short conclusion: computing many million times the intersections between a Point and a Polygon defined by some hundredth thousands Vertices is a damn hard computational problem.
And consequently it requires a very long time, so long to be absolutely unpractical.

A second attempt based on ST_Subdivide() and VirtualElementary

CREATE TABLE xx (id INTEGER PRIMARY KEY);
SELECT AddGeometryColumn('xx', 'geom', 3003, 'MULTIPOLYGON', 'XY');
INSERT INTO xx VALUES (1, NULL);

We'll start first by creating a convenience Table intended to temporarily store the result of ST_Subdivide(). This Table is very simple:

it has just two columns, a Primary Key and a MultiPolygon Geometry.
and it's intended to store just a single row identified by id=1

UPDATE xx SET geom = (SELECT ST_Subdivide(geometry, 2048) FROM tuscany) WHERE id = 1;
SELECT Count(*)
FROM ElementaryGeometries AS t
JOIN civici AS c ON (ST_Intersects(c.geometry, t.geometry) = 1
     AND c.rowid IN (
         SELECT rowid FROM SpatialIndex
         WHERE f_table_name = 'civici' AND search_frame = t.geometry))
WHERE f_table_name = 'xx' AND origin_rowid = 1;
----------------
1480991 (in 38.094 seconds)


UPDATE xx SET geom = (SELECT ST_Subdivide(geometry, 512) FROM tuscany) WHERE id = 1;
SELECT Count(*)
FROM ElementaryGeometries AS t
JOIN civici AS c ON (ST_Intersects(c.geometry, t.geometry) = 1
     AND c.rowid IN (
         SELECT rowid FROM SpatialIndex
         WHERE f_table_name = 'civici' AND search_frame = t.geometry))
WHERE f_table_name = 'xx' AND origin_rowid = 1;
----------------
1480991 (in 12.617 seconds)


UPDATE xx SET geom = (SELECT ST_Subdivide(geometry) FROM tuscany) WHERE id = 1;
SELECT Count(*)
FROM ElementaryGeometries AS t
JOIN civici AS c ON (ST_Intersects(c.geometry, t.geometry) = 1
     AND c.rowid IN (
         SELECT rowid FROM SpatialIndex
         WHERE f_table_name = 'civici' AND search_frame = t.geometry))
WHERE f_table_name = 'xx' AND origin_rowid = 1;
----------------
1480991 (in 9.534 seconds)

Quick evaluation:

ST_Subdivide definitely is the tool of the trade we were searching for.
It effectively allows to resolve a computationally hard problem in a surprisingly quick time.
Passing from many long hours to just a handful of seconds is a simply astonishing improvement.
subdividing the initial huge Polygon into many simpler/smaller parts has several beneficial effects:
- the time required to compute a point-to-polygon intersection quickly increases with the number of Vertices.
  Smaller polygons are obviously much more faster to be evaluated than bigger ones.
- smaller polygons doesn't shadow the Spatial Index, that can be efficiently queried.
using VirtualElementary in order to process all sub-parts one by one surely imposes some further complexity to our SQL queries.
But at the end of the day it confirms to be a very efficient mechanism.
Note: SpatiaLite is not PostGIS, and SQLite3 is not PostgreSQL; their respective internal architectures significantly differ under many aspects.
More specifically, SQLite is completely unable to support arrays or multi-row results, so using VirtualElementary is an absolutely necessary workaround.

A final experimental attempt based on a pure SQL approach

There is an alternative mechanism based on pure SQL and not requiring to use nor ElementaryGeometries neither a convenience Table:

WITH RECURSIVE magic(n, geom) AS (
    VALUES(1, (SELECT ST_Subdivide(geometry, 2048) FROM tuscany))
    UNION ALL
    SELECT n + 1, geom
    FROM geom_ind
    WHERE ST_GeometryN(geom, n) IS NOT NULL
)
SELECT n, ST_GeometryN(geom, n) FROM magic;

we simply have to write a Recursive SQL Query in order to get a multi-row resultset, with a distinct row for each elementary part.
it effectively works, but seems to be slower than ElementaryGeometries.
and even more relevant, I was unable to write a complete Query determining all intersections between Points and Polygons in a reasonable time.
I can simply suppose that the Query Optimizer of SQLite will end up in ignoring the Spatial Index, thus completely vanishing the usefulness of this approach.
May well be that someone else could succeed where I failed; any further third-party investigation on this specific area is surely welcome.

back to index