SpatiaLite: circles-ellipses

New SQL functions supporting Circles and Ellipses introduced in 4.1.0

MakeCircle ( cx, cy, radius ) MakeCircle ( cx, cy, radius, srid ) MakeCircle ( cx, cy, radius, srid, step ) Will return a closed Linestring approximating a circle. cx and cy are the coordinates identifying the centre. both radius and srid are self-explanatory. the optional argument step defines how many points will be interpolated on the curve. step corresponds to an angular distance measured in degrees; two consecutive points will be separated by this distance.	SELECT MakeCircle(0, 0, 100, -1, 1);
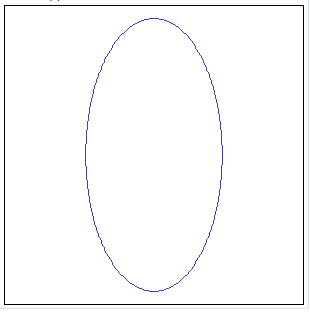
MakeEllipse ( cx, cy, x_axis, y_axis ) MakeEllipse ( cx, cy, x_axis, y_axis, srid ) MakeEllipse ( cx, cy, x_axis, y_axis, srid, step ) Will return a closed Linestring approximating an ellipse. cx, cy, srid and step have exactly the same identical meaning as before. x_axis and y_axis define respectively the horizontal and vertical axes of the ellipse.	SELECT MakeEllipse(0, 0, 100, 50, -1, 1);	SELECT MakeEllipse(0, 0, 50, 100, -1, 1);
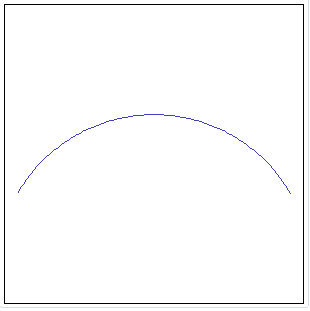
MakeArc ( cx, cy, radius, start, stop ) MakeArc ( cx, cy, radius, start, stop, srid ) MakeArc ( cx, cy, radius, start, stop, srid, step ) Will return a Linestring approximating a circular arc. cx, cy, radius and step are exactly as above. start and stop define the extreme points of the arc; both are angles expressed in degrees. The arc will be always drawn in counterclockwise direction.	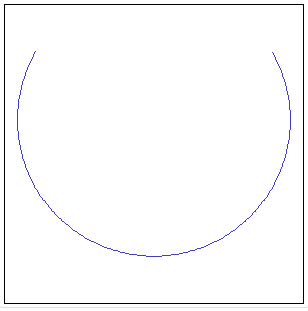SELECT MakeArc(0, 0, 100, 30, 150, -1, 1);	SELECT MakeArc(0, 0, 100, 30, 150, -1, 1);
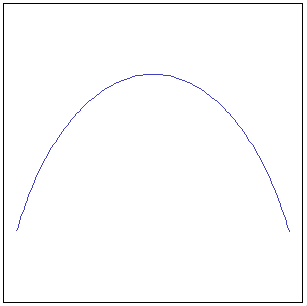
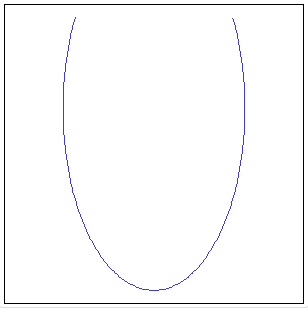
MakeEllipticArc ( cx, cy, x_axis, y_axis, start, stop ) MakeEllipticArc ( cx, cy, x_axis, y_axis, start, stop, srid ) MakeEllipticArc ( cx, cy, x_axis, y_axis, start, stop, srid, step ) Will return a Linestring approximating an elliptic arc.	SELECT MakeEllipticArc(0, 0, 50, 100, 30, 150, -1, 1);	SELECT MakeEllipticArc(0, 0, 50, 100, 150, 30, -1, 1);
MakeCircularSector ( cx, cy, radius, start, stop ) MakeCircularSector ( cx, cy, radius, start, stop, srid ) MakeCircularSector ( cx, cy, radius, start, stop, srid, step ) Will return a Polygon approximating a circular sector.	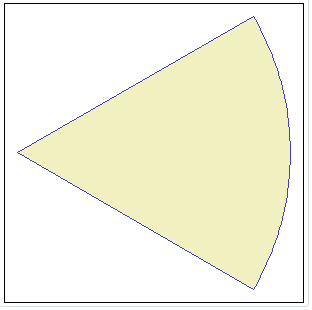SELECT MakeCircularSector(0, 0, 100, 330, 30, -1, 1);	SELECT MakeCircularSector(0, 0, 100, 30, 330, -1, 1);
MakeEllipticSector ( cx, cy, x_axis, y_axis, start, stop ) MakeEllipticSector ( cx, cy, x_axis, y_axis, start, stop, srid ) MakeEllipticSector ( cx, cy, x_axis, y_axis, start, stop, srid, step ) Will return a Polygon approximating an elliptic sector.	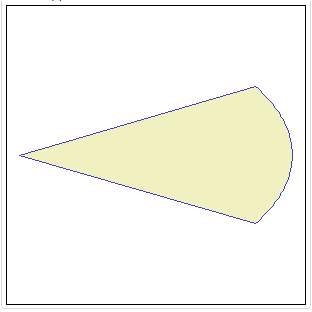SELECT MakeEllipticSector(0, 0, 100, 50, 330, 30, -1, 1);	SELECT MakeEllipticSector(0, 0, 100, 50, 30, 330, -1, 1);
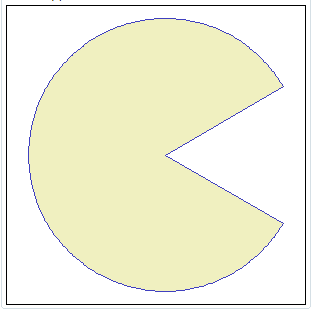
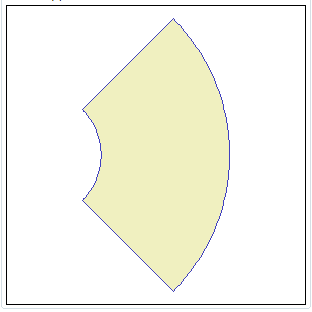
MakeCircularStripe ( cx, cy, radius_1, radius_2, start, stop ) MakeCircularStripe ( cx, cy, radius_1, radius_2, start, stop, srid ) MakeCircularStripe ( cx, cy, radius_1, radius_2, start, stop, srid, step ) Will return a Polygon delimited by two circular arcs sharing the same centre but having different radii.	SELECT MakeCircularStripe(0, 0, 100, 90, 45, 315, -1, 1);	SELECT MakeCircularStripe(0, 0, 50, 150, 315, 45, -1, 1);
Any function supporting circles and ellipses could obviously be nested with any other Spatial SQL function so to get more elaborate results. e.g. RotateCoords() and ShiftCoords() could be invoked in order to apply an arbitrary roto-translation.	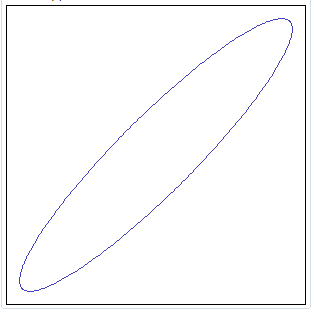SELECT RotateCoords( MakeEllipse(0, 0, 100, 20, -1, 1), 45);

back