OGC-SFS Geometries
As you already know, the standard representation of Geometries supported by any existing Spatial DBMS is based on the following SFS classes (non-topological):
- (MULTI)POINT
- (MULTI)LINESTRING
- (MULTI)POLYGON
- GEOMETRYCOLLECTION
Topology-Geometry
The international standard ISO/IEC 13249-3 (Information technology -- Database languages -- SQL multimedia and application packages -- Part 3: Spatial aka SQL/MM) defines a radically different Geometry model named Topology-Geometry based on the following primitives:
- a NODE simply is a notable point, and can be assumed to
be equivalent to SFS POINT.
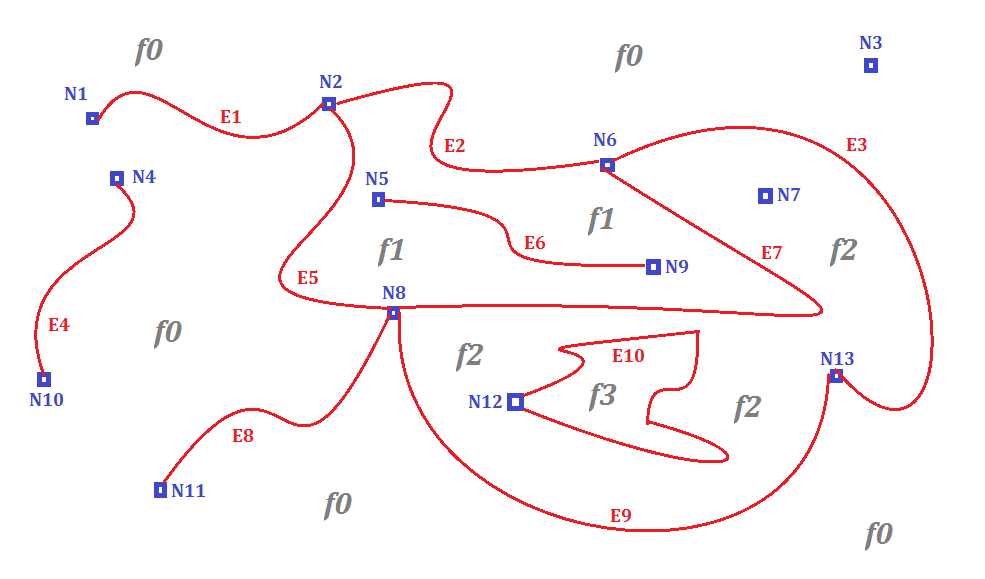
Examples: N1, N2, N3, ... N12, N13
- an EDGE is an oriented path joining two nodes, and can
be assumed to be equivalent to SFS LINESTRING.
Examples: E1, E2, E3, ... E8, E9
- a FACE is a portion of the plane delimited by edges,
and can be assumed to be equivalent to SFS POLYGON.
Examples: f0, f1, f2, f3
A very special Face is always implicitly assumed to exist on any Topology: it's the Universal Face (aka f0), and it's assumed to contain everything else exterior to all other Faces. So a completely empty Topology-Geometry will always contain at least the Universal Face.
Nodes N3 and N7 are someway special because they are not connected to any Edge; they are examples of Isolated Nodes.
Edges E4 and E6 are special too, because they are not connected to any other Edge; they are examples of Isolated Edges. Edge E10 isn't an Isolated Edge because it separates Faces f2 and f3.
Both Nodes and Edges have an explicit Geometry, respectively of the POINT and LINESTRING type.
Faces will never directly have a Geometry and will always be internally represented by a corresponding list of delimiting Edges: e.g. Face f1 is delimited by Edges E2, E7, E5 and Face f2 is delimited by Edges E3, E9, E7 and E10.
|
|
Consistency requirements for ISO Topology-Geometry
- all topological complexes are fully decomposed into their topological primitives.
- no two nodes exist at the same position in space.
- a node exists at the beginning and end of every edge.
- no edge has a geometry which crosses the geometry of a node.
- no edge has a geometry which crosses, overlaps, or is contained within the geometry of another edge.
- all edge geometries are simple.
- all edge geometries have a start point equal to the geometry of their start node.
- all edge geometries have a end point equal to the geometry of their end node.
- no face has a geometry which overlaps the geometry of another face.
- no face has a geometry within the geometry of another face.
- a universal face exists.
- a valid polygon geometry can be constructed for all faces except the universal face.
- all geometries for the topology have the same spatial reference system.
|
|
|
Topology-Network
The same standard ISO/IEC 13249-3 (SQL/MM) defines a second type of Topology mainly intended for linear applications named Topology-Network and based on the following primitives:
- a NODE simply is a notable point, and can be assumed to
be equivalent to SFS POINT.
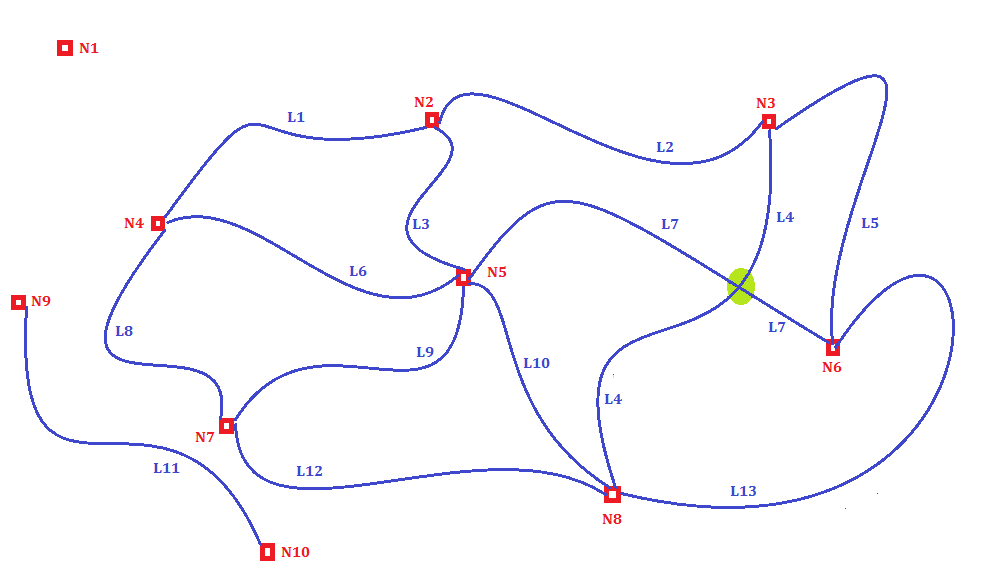
Examples: N1, N2, N3, ... N9, N10
- a LINK is an oriented path joining two nodes, and can
be assumed to be equivalent to SFS LINESTRING.
Examples: L1, L2, L3, ... L12, L13
Node N1 is an example of Isolated Node.
Link L11 is an examples of Isolated Link.
Please note: Links L4 and L7 do apparently cross (evidenced in the figure by a small green circle), but there is no Node corresponding to the intersection point.
This is a fully legitimate option supported by Topology-Network, and simply means that some restriction forbids a real intersection between the two Links.
There is an only apparent spatial junction, but there isn't any functional junction and consequently switching between Links L4 and L7 is strictly forbidden.
Possible examples: imagine two roads one overpassing/underpassing the other, or suppose an ordinary road junction where turning left/right is strictly forbidden by traffic regulations.
In an telecommunication network you can imagine two wires crossing under strict electric insulation conditions, and so on.
Accordingly to the ISO specifications, there are two different kinds of Topology-Networks:
- Logical Network: a network defined by connectivity informations but lacking any geometry information.
In other words, both Nodes and Links are always forbidden to have an explicit geometry.
- Spatial Network: a network defined by both connectivity and geometric informations.
In this second case both Nodes and Links are always expected to have an explicit Geometry, respectively of the POINT and LINESTRING type.
|
|
Consistency requirements for ISO Topology-Network - Spatial Network
- all topological complexes are fully decomposed into their topological primitives.
- all edge geometries have a start point equal to the geometry of their start node.
- all edge geometries have a end point equal to the geometry of their end node.
- all geometries for the topology have the same spatial reference system.
|
|
|